Goals and Outcomes
In this project you will create a simulation for a Newton’s Cradle (see visualization below). A Newton’s cradle is a series of pendula that display a “chain reaction” when each pendulum knocks into the pendulum next to it. This project involves some super cool - and fundamental! - physics concepts like angular momentum and conservation of momentum, which you can see in the Physics appendix. If you want some intuition for what you’re building in this project, we recommend skimming through this section now if you want to understand what you’re dealing with!
In this project, you will create pendula based on information drawn from your own Google Sheets spreadsheet!
The project uses VPython to implement the visualization.
What is VPython
VPython is a library that is designed to help write physics simulations, since it allows us to build and visualize objects, and also has a built-in mathematical library (including trigonometry, vectors and math operations).
VPython Objects
You can think of VPython’s box, sphere, and cylinder as the shapes that we get to see in the final visualization. Specifically, the shapes we use to create the pendulum are:
-
boxfor the axle (support) -
spherefor the bob (mass hanging in the pendulum) -
cylinderfor the cord (string of the pendulum)
To customize the bobs, we use VPython’s textures and colors, which are initialized in constants.py. The TEXTURE_MAP dictionary contains the textures, and the COLOR_MAP dictionary
contains the colors. These have been used in pendulum.py (which is provided to you), but you will end up working with these objects; so it is good to know where they came from!
When working with box, sphere, and cylinder, you can use their specific attributes to access information. For example, if we have ball = sphere(...), then we can use ball.radius to get
ball’s radius and ball.pos to get ball’s position (as a vector).
We have provided additional documentation on the attributes of various VPython objects if you would like to read it.
VPython Math
VPython uses vectors to define the axes and positions. It uses something called “operator overloading” to allow us to add and multiply vectors exactly like we do with numbers!
This is the same thing that allows us to use + with both strs and ints!
To find the magnitude of a given vector vec, you can use the function mag(vec). You can also directly use trigonometric functions like sin(theta) where theta is in radians.
Setup
The first thing you need to do is set up the Google Sheets spreadsheet and authentication for this project. You should begin by following the setup instructions here.
The setup is very important for this project to work at all, so make sure it’s the first thing you do! If you have any trouble with it, we encourage you to come to Office Hours.
Task 0.
Follow the setup instructions for Google Sheets very carefully. Then, go to constants.py and fill in the following information:
- The range in the spreadsheet we are looking at (
RANGE). The range of the spreadsheet is a string that represents the grid of cells you will be using. For example,RANGE= “A1:D5” will cover all the cells in the first 4 columns (A-D) and the first 5 rows (1-5) - The spreadsheet’s unique ID (
SPREADSHEET_ID), which can be found in the url of the Google Sheet:https://docs.google.com/spreadsheets/d/<<SPREADSHEET_ID>>/edit?gid=0#gid=0
Newton’s Cradle Simulation
Once you have finished setting up Google Sheets and filled in the 2 fields in constants.py as mentioned above, you are ready to begin implementing your own simulation!
For this part, you will be working in visualize_cradle_run.py. You have been provided some functions and others that are partially filled to use throughout this project. These functions are described
as they become relevant in this guide.
Now, you can begin filling this file out function by function in accordance with our descriptions below!
The return value of get_pendulum_info is a pend_list.
For most of these files, you will be working with a list of pendulums, each of which is a dictionary
containing corresponding to a pendulum.
If you are confused about what a pendulum dictionary looks like or want more information at any
point as you work on this file, we highly encourage you to try using print statements on
pend_list to look for yourself!
Pendulum Creation (D Tests)
In the first part of the project, we will focus on actually building the pendulum and setting up the physical attributes to use in the rest of the program.
To correctly update the spreadsheet, your values need to be in the form of a nested list. That is to say, it needs to be a list of lists, where the values in each inner list populate the cells in a row - so the number of inner lists corresponds to the number of rows, and the number of items in each inner list corresponds to the number of columns for that row.
You can update any rectangular range of cells as long as you stick to this format. For example, providing the update values [[1.5,2], [1,1.5]] for the range “A2:B3” would populate the sheet as:

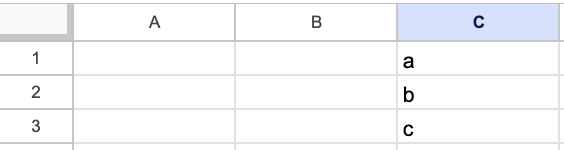
and providing the update values [['a'], ['b'], ['c']] for the range “C1:C3” would populate the sheet as:
You will start by implementing four short functions in the file special_cradles.py:
uniform_mass_newton_cradle(spreadsheet_id, mass_range, mass, num_pends)
Updates the spreadsheet corresponding to the spreadsheet_id using a helper function from sheets_api.py, such that all the mass values in the specific column range of cells mass_range are assigned the value mass.
uniform_e_newton_cradle(spreadsheet_id, e_range, e_val, num_pends)
Updates the spreadsheet corresponding to the spreadsheet_id using a helper function from sheets_api.py, such that all the coefficients of restitution in the specific column range e_range are assigned a provided e value.
elastic_newton_cradle(spreadsheet_id, e_range, num_pends)
Update the spreadsheet and uniformly assigns all pendula with the elastic restitution coefficient value.
Hint: Do not duplicate code you’ve already written.
inelastic_newton_cradle(spreadsheet_id, e_range, num_pends)
Updates the spreadsheet and uniformly assigns all pendula with the inelastic restitution coefficient value.
Hint: Do not duplicate code you’ve already written.
Task 1.0.
Implement the functions uniform_mass_newton_cradle, uniform_e_newton_cradle, elastic_newton_cradle, and inelastic_newton_cradle as described above. The docstrings in the starter code will
be helpful for you to get a hang of how things work.
make_newton_cradle(ranges, spreadsheet_id, r_param, theta_init)
Creates the list of pendulum dictionaries pend_list, using a helper function from sheets_api.py, with the provided ranges of the relevant cells in the spreadsheet, and the unique spreadsheet_id.
You should use the following algorithm:
- In a
forloop, update each pendulum dictionary inpend_listto include the following 3key: valuepairs.-
theta: the angle of the pendulum with respect to normal (perpendicular to theaxle). It should betheta_initfor the first pendulum, and0for all the others. -
omega: the angular velocity, which should be0for all the pendula. -
pendulum: atupleof the(axle, bob, and cord)VPythonobjects that constitute the actual pendulum itself- To find the ‘color’ and ‘texture’ strings of the pendulum from the Google Sheet, use the pendulum dictionary.
- Then, use the
COLOR_MAPandTEXTURE_MAPrespectively (fromconstants.py) to find theVPythoncolor and texture objects to which these strings map. - The axle position of the $i$th pendulum can be defined as
axle_pos = vector((-0.1+r_param/4 * i), r_param/5, 0). - Finally, use one relevant helper function from
pendulum.pyto create the pendulum tuple with the(axle, bob, and cord), which will be the value of the keypendulum.
-
- Return the updated
pend_list.
Task 1.25.
Implement the remaining function, make_newton_cradle (also in the file special_cradles.py), as described above. The docstrings in the starter code will (still) be helpful for you to get a hang of how things work.
You can ignore those.
We’ve added some types so you can see which keys and values in your dictionary are required, but Pyright doesn’t always infer those types correctly. Feel free to ask if you are curious why.
Task 1.5.
To test your code, click the beaker on the left side of vscode. After a few seconds, you should see a tree with project04-YOURUSERNAMAE at the top! Click the play button on the right, and then open up the list of tests using the arrow on the left side of that tree. Finally, find the subtree 0.D > test_task_1.py. All of the tests inside this part should be passing.
Additionally, by running the D tests, you should be able to see a visualisation of the Newton’s cradle in your browser! Don’t worry if the visualisation only lasts a few seconds, or if the browser tab closes automatically. If the visualisation tab hasn’t closed in your browser, you can close it to end the tests.
Swing Implementation (C Tests)
In the second part of the project, you will focus on the functionality of each individual pendulum; specifically, how each pendulum swings. You will implement that functionality for the entire cradle. The following three functions are all located in the file swinging.py.
angle_update(omega, theta, r_param, dt, g)
Takes in the current values of angle theta ($\theta$) and angular velocity omega ($\omega$) and updates them for a given timestep dt and gravitational acceleration g. Returns a tuple of the new $(\omega_{new}, \theta_{new})$.
Task 2.
Write the function angle_update(omega, theta, r_param, dt, g) described above. You should refer to the section “Angular momentum and velocity” for the relevant physical equations to calculate $\theta_{new}$ $\omega_{new}$, using the given values for theta, omega, g, and the length of the cord r_param.
Task 2.5.
Like before, click on the beaker. Following the same steps as before, this time, look for the 1.C > test_task2.py subtree, and make sure the tests are passing.
Next, you will write the function to update the each pendulum. We’ve provided a helpful function swing_update, which essentially performs a ‘swing’ of the pendulum.
It takes in the pendulum’s dictionary pend_dict, the length of the cord r_param, the time step dt, and the gravitational acceleration g and updates the angle and position of the pendulum components, using the helper function angle_update. The pend_dict is updated and nothing is returned.
full_swing_update(pend_list, r_param, dt, g)
Uses the helper function swing_update to each pendulum in the Newton’s cradle.
Hint: Use a for loop.
Task 3.
Write the function full_swing_update(pend_list, r_param, dt, g).
Task 3.5.
Like before, click on the beaker. Following the same steps as before, this time, look for the C > test_task3.py subtree.
By now, all the C tests should be passing. Ensure this is the case before moving on to the next section!
Handling Collisions (B Tests)
In this part of the project, you will focus on what happens to the pendula when they knock into each other, which lies at the heart of the Newton’s cradle demonstration. Everything from now on will need to be written in visualize_cradle_run.py.
Specifically, you will implement the handle_collision function to the following specification:
handle_collision(e, omega1, omega2, m1, m2, r_param)
Takes in the initial angular velocities of both bobs (omega1 and omega2), their coefficient of restitution (e), their masses (m1 and m2),and the cord length r_param and returns a tuple of the new angular velocities of both bobs (new_omega1, new_omega2).
Task 4.
Implement handle_collision(e, omega1, omega2, m1, m2, r_param). You can refer to the section “Conservation Laws” for information on how to implement the physics of this.
Task 4.5.
Follow the same instructions for the tests as before, but this time with the 2.B > test_task4.py subtree.
Now we get to the longest function you will have to write, but we can break it down.
handle_two_bobs(pend1, pend2, r_param)
Handles the pairwise interactions between two bobs in the Newton’s cradle, including checking for and handling collisions.
Takes in two dictionaries (pend1 and pend2), representing the two pendula in the interaction.
- For each pendulum dictionary, get the masses, bobs and angular velocity (
omega). - From only the first dictionary, get the coefficient of restitution.
- Check if the magnitude of the difference in positions of both bobs is less than or equal to
1.05times the sum of the bobs’ radii. We add a little bit of buffer to what is considered a ‘collision’.- If
true, use the helper functionhandle_collisionto get the new angular velocity values for both pendula. - Then, update both dictionaries with their respective new
omegavalues.
- If
Keep in mind that all the information that was obtained from the Google Sheet (including masses and restitution coefficients) were all stored as strings. If you want to use any of the quantities
in a calculation, you will need to convert them to floats.
Task 5.
Implement the function handle_two_bobs(pend1, pend2, r_param) as described above.
As a reminder, you can access positions and radii of VPython objects with bob.pos and bob.radius, and magnitude using mag(vec).
Task 5.5.
Follow the same instructions for the tests as before, but this time with the B > test_task5.py subtree.
At this point, all the B tests should be passing with your code!
Running the Simulation (A Tests)
This is where you put everything you have written so far to use. Finally, in this part of the project, you will put everything together and get to see your simulation!
newton_cradle_tick(pend_list, r_param, dt, g)
Performs a single timestep or tick of the Newton’s cradle.
- Update the swings of all the pendula (Hint: Use a function you already wrote!)
- For each pendulum (except the last) handle the pairwise interaction of that pendulum and the one after it. (Hint: Use another function you already wrote!)
Task 6.
Implement the function newton_cradle_tick(pend_list, r_param, dt, g) as described above.
if __name__ == "main" (partially provided)
Runs when you press the triangular play button at the top right corner of your vscode window. It is the culmination of all the helper functions you have written, and creates the Newton’s cradle visualisation from data in the Google Sheets spreadsheet.
- Use a helper function you wrote before to create the
pend_listthat you will use for the entire Newton’s cradle. Remember to use the appropriate constants fromconstants.pywhen calling this function! - In the (partially provided)
whileloop (i.e., while the simulation is still running), call a helper function with arguments fromconstants.pyto perform a single tick of the Newton’s cradle.
Task 7. Finish implementing the main run sequence of the Newton’s Cradle Simulation, using the appropriate helper functions you wrote before.
Task 7.5.
As you have done previously, run the tests with the 3.A > test_task6.py subtree. Make sure you are passing all the A tests!
And that’s it - your entire Newton’s cradle simulation is ready!
You can customise your simulation by modifying the Google Sheet spreadsheet before making the Newton’s cradle, using any of the helper functions uniform_mass_newton_cradle, inelastic_newton_cradle, and elastic_newton_cradle to see the effects of uniform coefficients of restitution and masses on the system. You can also directly modify the spreadsheet and see the changes translate into your Newton’s cradle - so feel free to play around with the values!
Appendix: Physics Derivations!
The following physics is based on a pendulum that looks like this [2]:
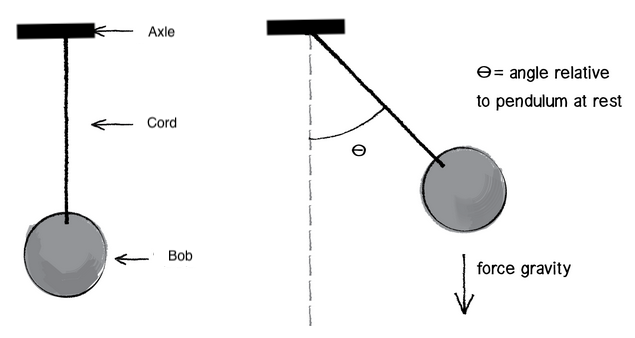
Angular Momentum and Velocity
For a swinging pendulum, we care more about the angular physical attributes than the linear ones. Thus, we have to work with:
Angular Acceleration
\(\dot{\omega} = \frac{-g \sin \theta}{R}\) where $g$ is the gravitational acceleration and $\theta$ is the angle formed by the cord normal to the axle.
Discrete Updates of the angular velocity with the angular acceleration
\(\omega_{new} = \omega + \dot{\omega} \Delta t\)
Updating the angle using the new angular velocity
\(\theta_{new} = \theta + \omega_{new} \Delta t\)
Conservation Laws
The Newton’s cradle is defined by the collisions between its pendula. The entire system should conserve kinetic energy in an elastic collision and conserve linear momentum (during a collision, we can approximate the momentum to be linear). We can approach the entire sequence of pendula in a pairwise manner, so we only consider the collision of two pendula. The two equations we have to take care of are:
Conservation of Linear Momentum
\(m_1 v_1 + m_2 v_2 = m_1 v_1^{new} + m_2 v_2^{new}\)
Conservation of Kinetic Energy
Kinetic energy is a little tricky to conserve when there is an elastic collision. We ask you to take in a quantity called coefficient of restitution $e$ which determines the “level” of inelasticity of a collision. If $e = 0$, it is a perfectly inelastic collision (kinetic energy not conserved), and if $e = 1$, it is a perfectly elastic collision (kinetic energy is conserved). We define:
\[e = \frac{v_2^{new} - v_1^{new}}{v_1 - v_2}\]Then, combining these equations, we can update the velocities of the objects post-collision as follows:
\[v_1^{new} = \frac{m_1 v_1 + m_2 v_2 - m_2 e(v_1 - v_2)}{m_1+m_2}\] \[v_2^{new} = \frac{m_1 v_1 + m_2 v_2 + m_1 e(v_1 - v_2)}{m_1+m_2}\]If we start off using angular velocities $\omega$, we need to convert them to linear velocities $v = R \times \omega$ for this equation, and the new calculated velocities can be converted back to angular velocities with the same equation.
Honor Roll Challenge
If you would like to challenge yourself even further, we have designed problems that that go beyond the course’s typical level of complexity. While these problems are entirely optional, we think some of you might enjoy pushing your limits. We will offer several of these challenges throughout the course assignments but you are in no way expected to complete them. You should expect much less guidance for those problems and cannot utilize TA Office Hours as our priority is to support students working on the main project. For general guidance or additional questions, please attend Professor Blank’s Office Hours.
If you’re still reading this, you have implemented the most basic version of the Newton’s cradle: a series of pendulums that collide with each other. However, we can add more degrees of freedom to the system to make it a little more complicated. For instance, we can make each element of the cradle a double pendulum, such that the first pendulum (cord1 and bob1) starts oscillating with angle theta and the second pendulum attached to it (cord2 and bob2) starts oscillating with angle phi.
Here is a picture of what we have described:

The next few steps to convert your Newton’s cradle into a double Newton’s cradle are:
- Define a
make_double_pendulum()that makes the double-pendulum structure with correctly calculated positions for all the components - Take in a
THETA_INITas well as aPHI_INITto define both angles of your double pendulum - Define a
double_angle_update()that updates both angles of the pendulum. Here, it is important to choose a valid reference frame - if you are looking at the entire system from a ‘lab frame’, the total angle of the bottom pendulum will actually be the sum ofTHETA_INITandPHI_INIT, but you can choose whatever reference frame works best for your understanding. You should update the positions accordingly.
Feel free to write any helper functions that make sense to you. You will likely have to do more work than described above (with slight changes to functions you have already written previously) to actually get the double pendulum to work as you expect it to.
When you demo your code, make sure your A tests still work before showing us your Honor Roll demo.
References:
- https://sites.ualberta.ca/~dnobes/Teaching_Section/Simulations/Newtons_Cradle/Simulation/Cradle.pdf
- Image credit: Khan Academy, “Trig and forces: the pendulum”. https://www.khanacademy.org/computing/computer-programming/programming-natural-simulations/programming-oscillations/a/trig-and-forces-the-pendulum
